Material Stiffness

1. Aféierung

Stiffness is a fundamental property in material science and engineering that dictates how a material or structure resists deformation under applied forces.

Whether constructing skyscrapers, designing lightweight aerospace components, or developing precise medical implants,

stiffness is critical in ensuring durability, Sécherheeten, and optimal performance.

This article delves into the concept of stiffness, exploring its types, influencing factors, testing methods, an Uwendungen, with practical insights for engineers and designers.

2. What is Stiffness?

Stiffness is a fundamental property that quantifies a material’s or structure’s resistance to deformation when subjected to an external force.

It plays a critical role in engineering and material science, dictating how structures behave under various loads and ensuring their integrity and performance.

Differentiating Stiffness from Related Terms

• Staang: While stiffness measures the ability to resist deformation, strength refers to the maximum stress a material can withstand before it fails or permanently deforms.
  A material can be stiff but not necessarily strong, and vice versa.
• Elasticity: Elasticity describes a material’s ability to return to its original shape after being deformed.
  All elastic materials exhibit some degree of stiffness, but stiffness specifically concerns the magnitude of force required to cause a given displacement.
• Hannscht: Hardness relates to a material’s resistance to localized surface indentation or scratching.
  Although related, hardness does not directly measure a material’s overall resistance to deformation under load.

Mathematical Representation of Stiffness

Mathematically, steifheet (k) is defined as the ratio of the applied force (F) to the resulting displacement (δ): k=F/δ

This relationship shows that higher stiffness means more force is required to achieve a certain amount of displacement.

A praktesche Begrëffer, a stiffer material or structure will deform less under the same load than a less stiff one.

3. Types of Stiffness

Steifheet, a critical property in material and structural design, refers to a material’s or structure’s resistance to deformation under applied forces.

Different types of stiffness address the ways materials and structures respond to various loading conditions.

Below are the primary types of stiffness:

Axial Stiffness

Axial stiffness refers to a material’s response to forces that act along its length, either in tension or compression.

This type of stiffness plays a crucial role in components like Socueles, Trägere, rods, an an Schëffster that must maintain their length and resist elongation or compression under load.

Formell:

The axial stiffness (k_a) is expressed as:

• k_a = EA/L

Wou !!!:

• • E is Young’s modulus,
  • A is the cross-sectional area,
  • L is the length of the material.

• Uwendungen:

• • Columns and Structural Elements: Axial stiffness ensures that columns can support vertical loads without excessive deformation.
  • Tensioned Cables: In bridges, suspension cables require high axial stiffness to maintain their structural integrity under tensile forces.

Rotational Stiffness

Rotational stiffness measures a material’s resistance to angular deflection or rotation when subjected to a torque or a moment.

This type of stiffness is vital for components that rotate or experience rotational loads, sou wéi Schëffster, Kupplungen, Beafingen, an an joints in mechanical assemblies.

Formell:

Rotational stiffness (k_r) is often expressed as:

• k_r = M/θ

Wou !!!:

• • M: is the applied torque,
  • θ: is the angular deflection.

• Uwendungen:

• • Fuert Schafe: In vehicles, rotational stiffness ensures the precise transmission of power without excessive twisting.
  • Bearings and Gearboxes: High rotational stiffness is essential in mechanical systems for smooth and controlled motion.

Lateral Stiffness

Lateral stiffness is the resistance of a material to forces that cause deformation perpendicular to its principal axis.

This type of stiffness is crucial for resisting sideways forces oder shear forces that may deform or destabilize a structure.

• Uwendungen:

• • Buildings and Bridges: Lateral rigidity ensures that structures can resist wind, seismic, and other lateral forces without excessive swaying or tilting.
  • Brécke: Maintaining lateral stability prevents deformation or failure under dynamic loads such as traffic or strong winds.

• Haaptun ze: In tall buildings, lateral stiffness is provided by shear walls, which prevent horizontal displacement due to wind or seismic activity.

Bending Stiffness

Bending stiffness refers to a material’s resistance to deformation under bending moments or forces that attempt to bend the material.

This is especially important in structural elements that experience bending, sou wéi Trägere, cantilevers, and slabs.

Formell:

The bending stiffness (k_b) is typically expressed as:

• k_b = EI/L^3

Wou !!!:

• • E is Young’s modulus,
  • I am the second moment of inertia of the cross-section (a measure of its resistance to bending),
  • L is the length of the beam or structure.

• Uwendungen:

• • Beams in Building Frames: Beams must resist bending to avoid deflection or failure under loads like floors, roofs, or machinery.
  • Cantilevers: In cantilevered structures (like bridges or overhangs), bending stiff is vital to maintaining stability and preventing excessive deflection.

Shear Stiffness

Shear stiffness refers to a material’s resistance to shearing forces, which act parallel to the surface and cause sliding or distortion of the material’s layers.

This is particularly important in components subjected to shear stresses, sou wéi shear walls and structural connections.

Formell:

Shear stiffness (k_s) is expressed as:

• k_s = GA/L

Wou !!!:

• • G is the shear modulus (a material property indicating its resistance to shear),
  • A is the cross-sectional area,
  • L is the length or thickness.

• Uwendungen:

• • Shear Walls: These are used in buildings and bridges to resist lateral forces and prevent structural failure.
  • Structural Connections: In mechanical assemblies, shear stiff is vital for ensuring that parts remain securely connected under loading conditions.

4. Factors Influencing Stiffness

Several factors influence the stiffness of a material or structure, and understanding these can help in selecting or designing materials for specific applications:

Material Eegeschafte:

• Elastic Modulus (Jonk Modul, E): This is the primary determinant of a material’s stiffness. Materials with higher Young’s modulus are stiffer. Zum Beispill, steel has a higher modulus than aluminum.

• Shear Modulus (G): For shear loads, the shear modulus plays a crucial role in defining shear stiffness.
• Poisson Verhältnis: Although less directly related, Poisson’s ratio affects how a material deforms in directions perpendicular to the applied load.
• Microstruktur: The internal structure of the material, including grain size, phase distribution, and presence of defects, can influence stiffness.
  Smaller grain sizes often increase stiffness due to grain boundary strengthening.

Geometry:

• Cross-sectional Area: A larger cross-sectional area increases axial rigidity but does not directly affect bending or torsional stiffness.
• Moment of Inertia (Ech): For bending, the second moment of area (or moment of inertia) of the cross-section is key.
  Increasing this value (by changing the shape or size of the cross-section) significantly increases bending stiffness.
• Polar Moment of Inertia (Jin): For torsion, the polar moment of inertia of the cross-section determines torsional stiffness.
• Length: Longer lengths decrease axial and bending rigidity but can sometimes increase torsional stiffness if the structure is properly designed.
• Form: The shape of the cross-section (Z.B., I-beam, tube, solid rectangle) affects how the structure distributes stress, thus influencing rigidity.

Support Conditions:

• Boundary Conditions: How a structure is supported or constrained can drastically alter its effective stiffness.
  Fixed supports increase stiff compared to simply supported or pinned ends.
• Connections: The stiffness of joints or connections can also influence the overall stiffness of an assembly or structure.

Zäitperei:

• Thermesch Expansioun: Temperature changes can cause thermal expansion or contraction, which might alter the dimensions and thus the stiffness of materials.
• Material Modulus: E puer Materialien, especially polymers, see a significant change in their modulus with temperature, affecting stiffness.

Load Type and Rate:

• Static vs. Dynamic Loads: Dynamic loads can result in different effective stiffness due to the rate of loading, schueden, and inertial effects.
• Frequency: At high frequencies, dynamic stiffness might differ from static stiffness due to resonance or damping effects.

Anisotropie:

• Material Directionality: In materials like composites, Holz., or some metals, rigidity can vary with direction due to the alignment of fibers, grains, or other structural elements.

Presence of Stress Concentrators:

• Notches, Holes, and Cracks: These can reduce the effective stiffness by concentrating stress and promoting deformation or failure at these points.

Age and Environmental Exposure:

• Acting: Am Zäitoflaf, materials can change embrittlement, which can affect their stiffness.
• Ëmweltfaktoren: Exposure to elements like moisture, UV light, Chemariantie, or extreme temperatures can alter material properties, including stiffness.

Composite Structures:

• Layup and Orientation: In composite materials, the arrangement and orientation of reinforcing fibers or layers can significantly affect the directional stiffness.
• Matrix and Reinforcement: The properties of both the matrix (Z.B., polymer) and the reinforcing materials (Z.B., carbon fibers) contribute to the overall stiffness.

Fabrication and Processing:

• Manufacturing Defects: Imperfections introduced during manufacturing can reduce stiffness.
• Hëtztbehandlung: This can alter the microstructure, thus changing the material’s rigidity.

Strain Rate:

• Rate Dependency: Some materials exhibit rate-dependent behavior, where their stiffness changes with the rate at which they are deformed.

5. Importance of Stiffness in Engineering Applications

Stiffness is a critical property in the field of engineering as it directly influences the performance, Haltbarkeet, and safety of materials and structures.

Understanding and optimizing stiffness are fundamental for engineers to ensure that designs can withstand external forces without excessive deformation.

Below are key engineering applications where stiffness plays a crucial role:

Baulibatiounen: Brécke, Skyscrapers, and Structural Stability

In civil engineering, stiffness is essential for maintaining the stability and safety of structures such as Brécke, Gebaier, an an skyscrapers.

Structural elements must be designed to resist a variety of forces, ganz agemaach wind, traffic loads, and seismic activity.

• Bridge Construction: Bridges must maintain their structural integrity under dynamic loads like vehicles, wind, and temperature fluctuations.
  Lateral stiffness is critical to prevent swaying and ensure the bridge doesn’t deform excessively under wind loads.
• Skyscrapers: High-rise buildings must resist lateral forces (wind, earthquakes) while minimizing deflection.
  The lateral stiff of the building’s core and its shear walls are crucial in ensuring it remains stable and safe for occupants.

Haaptun ze: The Burj Khalifa, the tallest building in the world, uses advanced materials and a carefully designed stiff structure to resist wind forces and the building’s weight.

Mechanical Systems: Schëffster, Quellen, and Gears

In mechanical engineering, stiffness plays a significant role in components such as Schëffster, Quellen, an an Gears.

The ability of these components to maintain their shape and resist deformation under load is vital for the system’s functionality and efficiency.

• Schëffster: Rotational stiffness ensures shafts rotate without excessive deflection or bending, which could lead to failure or inefficiency in power transmission.
• Quellen: In devices such as shock absorbers or suspension systems, stiffness determines how much force a spring can resist before deforming, which affects ride comfort and safety.
• Gears: Rotational stiffness in gears ensures accurate transmission of power without distortion, maintaining the precision of mechanical systems.

Haaptun ze: Car suspension systems rely on high spring stiff to absorb shocks from the road, ensuring a smooth ride and maintaining vehicle stability.

Aerospace and Automotive: Enhancing Performance and Safety

In the aerospace and automotive industries, stiffness directly impacts performance, Sécherheeten, and fuel efficiency.

The balance between lightweight design an an sufficient stiffness is crucial for achieving high-performance and energy-efficient vehicles and aircraft.

• Aircraft: Airplanes and spacecraft need to maintain structural integrity under both static and dynamic loads.
  A Fliger, bending stiffness of the wings, fuselage, and landing gear is essential to avoid unwanted deformations during flight.
• Automotiv: In cars, particularly in high-performance and electric vehicles, chassis stiff contributes to better handling, ride comfort, and crashworthiness.
  A stiff frame reduces vibrations and improves the overall driving experience.

Haaptun ze: Formell 1 cars are designed with extremely stiff carbon fiber chassis to minimize deflection
and enhance handling performance while maintaining an optimal balance of weight and strength.

Medizinesch Geräter: Ensuring Durability and Precision in Prosthetics and Implants

In the field of medical engineering, stiffness is a crucial property for ensuring the Haltbarkeet an an Präzisioun of medical devices such as Prosthetiker, implants, an an surgical tools.

• Prosthetics: Prosthetic limbs need to mimic the stiffness of natural bone to ensure proper functionality and comfort.
  The materials must also be stiff enough to withstand daily wear and tear without excessive deformation.
• Implantate: For implants such as joint replacements, maintaining the stiffness of the implant material is essential for stability, Haltbarkeet, and the avoidance of wear or failure under mechanical stresses.

Haaptun ze: Dental implants must possess a stiffness similar to that of natural teeth to ensure they can endure the forces involved in chewing and biting without failure.

Renewable Energy: Wind Turbines and Solar Structures

Stiffness also plays a significant role in renewable energy technologies, besonnesch an wind turbines an an solar power structures.
In these applications, stiffness affects the ability of components to resist forces such as wind or temperature variations while maintaining efficiency.

• Wind Turbines: The blades of wind turbines must be stiff enough to resist bending under high wind loads but flexible enough to optimize energy capture.
  Stiffness is also critical in the tower and foundation to support the entire structure.
• Solar Panels: Solar panels must maintain their shape and alignment to maximize energy generation.
  The frames and mounting systems need to be stiff enough to prevent deformation caused by wind or snow loads.

Electronics and Consumer Products: Miniaturization and Performance

An Elektronik an an consumer products, stiffness is vital for both functionality and durability.

Many modern devices are miniaturized, and maintaining stiffness is key to ensuring that they continue to function effectively under stress or wear.

• Smartphones and Tablets: In portable devices, stiffness is important to maintain structural integrity while reducing weight.
  The materials used in the body of the device need to be stiff enough to prevent bending or breaking from everyday use, such as being dropped or subjected to pressure.

• • Haaptun ze: Aluminum and high-strength plastics are commonly used for the housing of electronics because they balance stiffness with lightness.

• Consumer Appliances: Household items such as washing machines, refrigerators, and vacuum cleaners rely on components that must withstand repeated use without deforming.
  Zum Beispill, the motors, Sigel, and casings all require adequate stiffness to ensure long-term durability.

• • Haaptun ze: Vacuum cleaner casings are made from stiff materials to protect the internal components from external impacts.

6. Stiffness of metal Material Chart

Below is a chart showing the stiffness of some common metal materials:

	Modulus vun der Elastizitéit		Shear Modulus
Metal Alloy	GPa	10^6 Psi	Gpa	10^6 Psi	Poisson Verhältnis
Aluminium	69	10	25	3.6	0.33
Bram Emmach	97	14	37	5.4	0.34
Kupfer	110	16	46	6.7	0.34
Magnativ	45	6.5	17	2.5	0.29
Nickel	207	30	76	11.0	0.31
Stum	207	30	83	12.0	0.30
Titanium	107	15.5	45	6.5	0.34
Bungsteren	407	59	160	23.2	0.28

7. Testing and Measuring Stiffness

Testing and measuring stiffness is essential for evaluating the performance and structural integrity of materials and components.

Engineers use various methods to determine how stiff a material is and whether it can withstand the forces it will encounter during use.

Below are the common methods and tools used for testing and measuring stiffness.

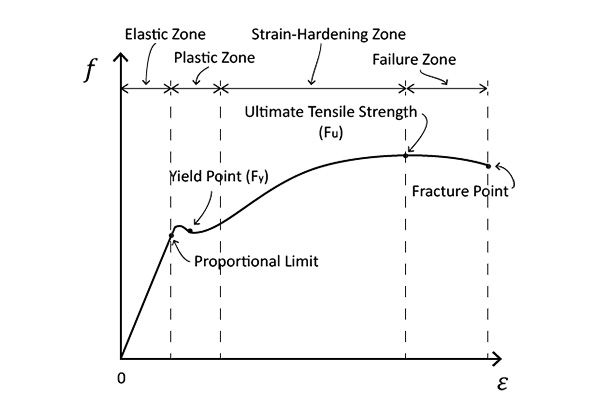
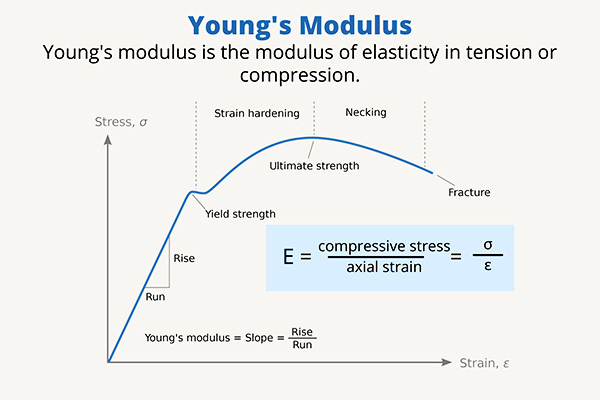
Tensile Testen

Tensile testing is one of the most widely used methods for determining the stiffness of a material, particularly for materials subjected to axial forces.

This test involves stretching a material sample to measure its stress-strain behavior.

• Sécherheet:
  The material sample is subjected to a tensile force applied at a constant rate. As the material stretches, its elongation is measured, and the corresponding force is recorded.
  The stiffness is determined from Jonk Modul, which is the ratio of tensile stress to tensile strain in the elastic region of the material’s behavior.
• Results:
  The stress-strain curve generated from the test provides key information about the material’s stiffness, Staang, and elasticity.
  The slope of the initial, linear portion of the curve represents the material’s Jonk Modul, which directly indicates its stiffness.
• Uwendungen:
  Tensile testing is commonly used in the Metallsaach, plastic, an an composite materials industries to evaluate the stiffness of materials for structural applications.

Kompressioun Testen

Compression testing is used to measure the stiffness of materials subjected to compressive forces.
This test is particularly useful for brittle materials like concrete, ceramics, and some metals.

• Sécherheet:
  A specimen is placed between two plates, and compressive force is applied along the specimen’s axis.
  The material’s Deformioun is measured as the load increases.
  The stiffness is determined by the modulus of elasticity under compression, similar to the tensile test.
• Results:
  The stress-strain curve obtained from the compression test provides data on the material’s ability to resist deformation under compressive forces.
  This is critical for evaluating structural elements that will experience compression, such as columns and beams in buildings and bridges.
• Uwendungen:
  This test is commonly used in civil engineering, Baulibatiounen, and materials science to evaluate concrete, bricks, masonry, an an Stum under compressive loading.

Flexural Testing (Bending Test)

Flexural testing, or bending testing, is used to measure the bending stiff of materials, especially beams, slabs, and plates.
It is particularly relevant for materials that will experience bending under load, sou wéi steel beams oder plastic panels.

• Sécherheet:
  A specimen is placed on two supports and a force is applied at the center of the specimen.
  The deflection at the center is measured, an den bending modulus (also known as the flexural modulus) is calculated based on the applied force and the deflection.

Results:
The bending stiffness is quantified by the flexural modulus.

• Uwendungen:
  Flexural testing is widely used for plastic materials, Komponites, an an Holz.,
  as well as for metal beams an an architectural components that need to maintain shape under bending forces.

Vibration Testing

Vibration testing measures stiffness based on the natural frequency of a material or structure.
The principle behind this method is that stiffer materials tend to have higher natural frequencies.

• Sécherheet:
  A test specimen is subjected to a vibration stimulus (such as a hammer strike or shaker), and its response is recorded using sensors.
  The natural frequency is determined, and stiffness is derived from the frequency response using analytical or numerical methods.
• Results:
  The resonant frequency can be used to calculate the dynamic stiffness of the structure or material.
  This method is particularly useful for evaluating large structures, machine components, an an components subjected to dynamic loading.
• Uwendungen:
  Vibration testing is commonly used in the Aerospace, Automotiv,
  an an construction industries to ensure that components can withstand dynamic forces without failure or excessive vibration.

Shear Testing

Shear testing measures the material’s resistance to shear forces and is used to evaluate the shear stiffness of materials like metals, Plastik, and adhesives.

• Sécherheet:
  The material is subjected to a shearing force, typically using a shear test apparatus such as a rheometer oder shear frame.
  The force required to cause a certain amount of displacement is measured, and the material’s shear modulus is calculated.
• Results:
  The test results provide information about the material’s ability to resist deformation under shear stresses.
  This is crucial for materials used in connections oder adhesive bonds that will experience shearing forces.
• Uwendungen:
  Shear testing is essential in industries like Baulibatiounen (for shear walls), Automotiv, an an adhesive bonding.

Digital Image Correlation (DIC)

Digital Image Correlation (DIC) as A non-contact optical method used to measure deformation in materials and structures.
It involves capturing high-speed photographs or video of a specimen during testing and analyzing the images to quantify the deformation.

• Sécherheet:
  The specimen’s surface is marked with a random pattern.
  As the material deforms under loading, A K) camera system captures images, and a computer system analyzes the displacement at each point on the surface.
• Results:
  DIC provides full-field displacement and strain data, offering a detailed understanding of how stiffness varies across a material under load.
• Uwendungen:
  DIC is commonly used in research an an development fir advanced materials, biomaterials, and complex structural systems that require detailed deformation analysis.

8. Balancing Stiffness with Other Properties

In engineering and material science, achieving the optimal balance between stiffness and other material properties
is crucial for designing components that meet specific performance, Sécherheeten, and cost requirements.

Stiffness vs. Flexibility

While stiffness refers to a material’s resistance to deformation, Flexibilitéit is the inverse — it describes a material’s ability to bend or stretch under load.

An e puer Uwendungen, flexibility is more desirable than stiffness, especially in situations where a material needs to absorb shock or accommodate movement.

• Haaptun ze: An Automotiv Suspension Systemer, materials with sufficient flexibility allow the system to absorb road vibrations and provide a smooth ride.
  Op der anerer Säit, in structural components like beams or supports, excessive flexibility can lead to Feeler oder excessive deformation, which is undesirable.

Trade-off: Materials with high stiffness (wéi Stol) are often less flexible, while materials like Gummel oder Plastik may exhibit more flexibility but less stiffness.
Engineers need to decide the right balance for each application.
Zum Beispill, in designing robotic arms, a balance between stiffness and flexibility is necessary to ensure precise movements without excessive rigidity.

Staang vs. Steifheet

Stiffness and strength are related but distinct properties.

Staang refers to a material’s ability to withstand an applied force without failure, heiansdo steifheet describes the material’s ability to resist deformation under an applied force.
An e puer Fäll, achieving a high level of stiffness might result in a reduction in strength, and vice versa.

• Haaptun ze: Titanium is a material known for both strength and stiffness, making it ideal for aerospace applications where both characteristics are critical.
  Wéi och ëmmer, overly stiff materials, sou wéi brittle ceramics, may crack or fail under high stress, even though they are resistant to deformation.

Trade-off: Materials with high stiffness often exhibit higher strength, but balancing this with Zougankheet (the ability to absorb energy before failure) ass essentiell.
Engineers often select materials based on the required strength-to-weight ratio for the application.

Stiffness vs. DUTTILITÉIT

DUTTILITÉIT refers to a material’s ability to deform under stress without breaking, typically by stretching or elongating.

Duktile Materialien, wéi hun Kupfer oder Aluminium, can absorb significant stress without cracking, making them ideal for applications where deformation is expected.

• Haaptun ze: An automobile crash structures, a balance between stiffness and ductility is important.
  The structure must be stiff enough to absorb and distribute the impact, but also ductile enough to deform safely and reduce the risk of injury to occupants.

Trade-off: Materials that are highly stiff, wéi hun Stum, tend to be less ductile, making them more prone to fracture under extreme stress.
Duktile Materialien, sou wéi Aluminium Ladionen, provide better deformation capabilities but may require thicker components to achieve similar stiffness.

Zougankheet vs. Steifheet

Zougankheet is a material’s ability to absorb energy and deform plastically before breaking.
Unlike stiffness, which resists deformation, toughness allows a material to withstand significant impacts or loads without failing.

• Haaptun ze: Materials like high-carbon steel have excellent toughness, which is critical in structural applications where impact resistance is necessary.
  Wéi och ëmmer, they may not have the same rigidity as Komponites used in lightweight applications.

Trade-off: In applications like sports equipment oder protective gear, engineers need to balance stiffness and toughness to ensure the material can absorb shock while maintaining structural integrity.
Too much stiffness might lead to brittle failure, while too much toughness might result in excessive deformation under load.

Stiffness vs. Middegkeet Resistenz

Fatigue resistance refers to a material’s ability to withstand repeated loading and unloading cycles without failure.
An e puer Uwendungen, a material may need to be both stiff and resistant to fatigue, sou wéi an aircraft components oder high-performance machinery.

• Haaptun ze: Titanium alloys are used in aerospace and medical applications because they combine high stiffness with excellent fatigue resistance.
  Op der anerer Säit, materials like Zoss may exhibit high stiffness but poor fatigue resistance, making them unsuitable for dynamic loading applications.

Trade-off: Highly stiff materials may be more susceptible to fatigue if they are brittle or prone to cracking under cyclic stresses.
Komponites, which are often used in aerospace, offer a good balance of stiff and fatigue resistance by combining stiffness with flexibility in specific orientations.

Stiffness vs. Thermesch Eegeschaften

Materials’ thermal properties, sou wéi thermesch Expansioun an an thermesch Verwaltungsgeschäfter, also play a role in balancing stiffness.
Thermal expansion refers to how a material changes in size when exposed to temperature changes.
If a material with high stiffness also has high thermal expansion, it may experience unwanted stresses when exposed to temperature fluctuations.

• Haaptun ze: In applications like Elektronik oder Motor Komponente, it is important to balance the stiffness of materials with their thermesch Stabilitéit.
  Materials like ceramics an an Komponites have low thermal expansion and high stiffness, making them ideal for high-temperature applications.

Trade-off: A highly stiff material with significant thermal expansion may suffer from thermesch Stress, which can cause cracking or deformation.
Am Kontrast, low-stiffness materials may deform easily under thermal loading, but they often experience less thermal stress.

9. How to Design for Good Stiffness?

Designing for good stiffness is a fundamental part of engineering, particularly when it comes to ensuring the performance, Sécherheeten, and longevity of components and structures.

Stiffness plays a critical role in how a material or structure resists deformation under applied loads.

Whether you are designing a bridge, A K) mechanical part, or an automotive component, achieving the right balance of stiffness is crucial.

An dëser Sektioun, we explore key considerations and strategies for designing for optimal stiffness.

Understand the Requirements of the Application

The first step in designing for good stiffness is to clearly understand the specific requirements of the application.

Steifheet needs can vary dramatically depending on the intended use, Ëmwelt, and loading conditions.

Zum Beispill, A K) high-performance car component may require a material that balances both stiffness and weight reduction,

while a structural beam for a building must prioritize stiffness to avoid excessive deflection or bending.

• Haaptun ze: An Aerospace Uwendungen, lightweight materials with high stiffness are often needed to withstand high loads while minimizing weight.
  Am Kontrast, fir Brécke oder high-rise buildings, Stum oder reinforced concrete with higher stiff values is preferred for its ability to resist large forces and maintain stability.

By identifying the primary performance goals — such as load-bearing capacity, dynamic response, an an safety margins — you can determine the optimal stiffness required for your design.

Select the Right Material

The material chosen for a design will play a crucial role in determining the stiffness of the final product.

The modulus of elasticity (oder Jonk Modul) is the primary material property that influences stiffness.

Materials with a high modulus of elasticity, sou wéi Stum, Titanium, and certain Komponites, offer high stiffness, while those with a lower modulus,

wéi hun Gummel oder Plastik, are more flexible but less stiff.

When selecting materials, betruecht:

• Mechanesch Eegeschafte: Evaluate the material’s stiffness, Staang, Middegkeet Resistenz, and other relevant properties.
• Gewiicht Considératiounen: In applications like automobiles oder Aerospace, materials with high stiffness-to-weight ratios,
  sou wéi Aluminium an an carbon fiber composites, are often preferred to reduce the overall weight of the structure.
• Cost and Availability: High-stiffness materials like Titanium oder fortgeschratt Komposit may be expensive, so consider trade-offs based on the project budget.

Optimize Geometry and Design

The geometry of the component — such as its shape, Gréisst, and cross-sectional area — significantly impacts its stiffness.

Engineers use several strategies to optimize the design for maximum stiffness while ensuring functionality and cost-efficiency.

• Moment of Inertia: The second moment of area (also known as area moment of inertia) is a critical factor in bending stiffness.
  Zum Beispill, A K) beam with a larger cross-sectional area or a reinforced shape (Z.B., I-beam or box section) will have a higher moment of inertia and thus greater stiffness.
• Shape Optimization: Tapered beams, hollow structures, an an ribbed designs can be used to provide stiffness where it’s needed most, without adding unnecessary material weight.
• Length-to-Diameter Ratios: For components like Socueles oder Schëffster, reducing the length-to-diameter ratio can increase stiffness.
  Shorter, thicker members typically provide better resistance to bending and deformation.
• Use of Reinforcements: Reinforcing ribs oder internal supports in a structure can significantly increase stiffness.
  Zum Beispill, composite panels used in aerospace are often designed with internal ribbing to maintain stiffness while keeping weight low.

Address Boundary Conditions and Loading

The way a structure is supported or fixed in place (boundary conditions) and the types of loads it will experience (static, dynamic, or cyclic) play a significant role in determining the stiffness of a system.

• Fixed Supports: Structures with fixed oder clamped supports are less likely to deflect compared to those that are simply supported or free at one end.
  The placement of supports and constraints influences how the material will deform under load.
• Load Distribution: Evenly distributed loads result in lower bending moments and deflections, while concentrated loads can cause more localized deformation.
  In designing for stiffness, it’s important to consider how the load is applied and distribute it as evenly as possible to minimize deformation.
• Dynamic Loads: If the component experiences vibrations oder cyclic loading, ensuring that the structure remains stiff while avoiding resonance or fatigue is critical.
  This often involves using materials with good fatigue resistance and designing for the appropriate damping.

Incorporate Safety Factors and Considerations for Variability

When designing for stiffness, engineers must also account for factors such as material variability, environmental changes (Z.B., Zäitperei, fiichtegkeet), an an safety margins.

Materials may have slight variations in their mechanical properties, and external conditions may influence their behavior under load.

• Safety Factors: Engineers often apply safety factors to account for uncertainties in loading conditions, material strength, and potential for failure.
  Zum Beispill, an Aerospace oder civil engineering, designs are often built to be significantly stiffer than the bare minimum requirements to ensure performance under unexpected circumstances.
• Environmental Effects: Consider how changes in Zäitperei, fiichtegkeet, or exposure to chemicals could affect the stiffness of the material.
  Thermal expansion is an example where temperature changes could influence the material’s stiffness, so these factors should be incorporated into the design.

Use Simulation and Optimization Tools

Modern engineering tools such as Finite Element Analysis (Fea) allow designers to simulate and test how different materials and geometries will behave under various loading conditions.
These tools can provide invaluable insights into:

• Stress distribution
• Deflection patterns
• Failure modes

Using FEA, engineers can iterate quickly on design concepts to optimize stiff while ensuring other critical factors, sou wéi Käschte, gewun Du, an an Performech, are also addressed.

Ganz nachelesch, optimization algorithms can suggest changes to geometry, material Auswiel, and loading conditions that will provide the best stiffness performance for the given constraints.

11. Consider ZDEZE Machining Services

DEZE provides expert machining services tailored to meet stiffness requirements in your designs.
With cutting-edge technology and precision engineering, ZDEZE ensures your components achieve the perfect balance of stiffness, Staang, and functionality.

12. Conclusioun

Stiffness is more than just a material property—it’s a critical factor in designing safe, muer ee grasting, and high-performing systems.

By understanding stiff and leveraging advanced materials and designs, engineers can create optimized solutions for a wide range of applications.

Ready to bring your project to life? Contact DEZE today for expert machining solutions designed to meet your stiffness needs.